Listed below are some publications and projects on which I am currently working. I find quantum error correction, quantum cryptography, and circuit qed fascinating! If you would like to discuss any of these projects or find any mistakes, feel free to contact me at cameron (dot) cianci @ gmail (dot) com
Publications
Latent Orthonormal Contrastive Learning in Disaster Damage Assessment Using Paired Remote Sensing Imagery
(Under Review to ICCV 2023)
Abstract: Error correction has long been suggested to extend the sensitivity of quantum sensors into the Heisenberg Limit. However, operations on logical qubits are only performed through finite sized universal gate sets such as Clifford+T. Although this approach may allow for universal quantum computation, the finite gate sizes present a problem for applications such as quantum sensing, since the signal must act continuously. The difficulty in constructing a continuous logical operator comes from the Eastin-Knill Theorem, which prevents it from being transverse. Since error correction is needed to approach the Heisenberg Limit, it is important to explore how to construct continuous logical operators. In this paper, a protocol to design a continuous logical Z-rotation (phase gate) is proposed and applied to the Steane Code. The fault tolerance of the designed operator is investigated using the Knill-Laflamme Conditions. The Knill-Laflamme Conditions indicate that diagonal unitary operator constructed cannot be fault tolerant due solely due to the possibilities of X errors on the middle qubit. The approach designed, however, may find success in codes with more qubits such as the Shor code, distance 3 surface code, [15,1,3] code, or codes with a larger distance such as the [11,1,5] code.
Abstract: Fourier acceleration is a technique used in Hybrid Monte Carlo simulations to decrease the autocorrelation between subsequent field configurations in the generated ensemble. It has been shown, in the perturbative limit, to eliminate the problem of critical slowing down in a phi^4 theory. As a result, there are several techniques that are being explored to generalize Fourier acceleration to work with non-Abelian gauge theories like QCD. It is hoped that these methods will prove effective at overcoming the problem of critical slowing down, even in the non-perturbative limit. In our work, we show that Fourier acceleration can be applied effectively to a linear sigma model in the symmetry broken phase, leading to reduced autocorrelation and faster thermalization. We present an algorithm for estimating the optimal Fourier acceleration masses dynamically, based on the lattice data. In the future, we hope to explore the effectiveness of these techniques in the strongly-interacting case. Since our phi^4 theory is a linear chiral effective theory for QCD, this could be interesting for those seeking to generalize Fourier acceleration to QCD.
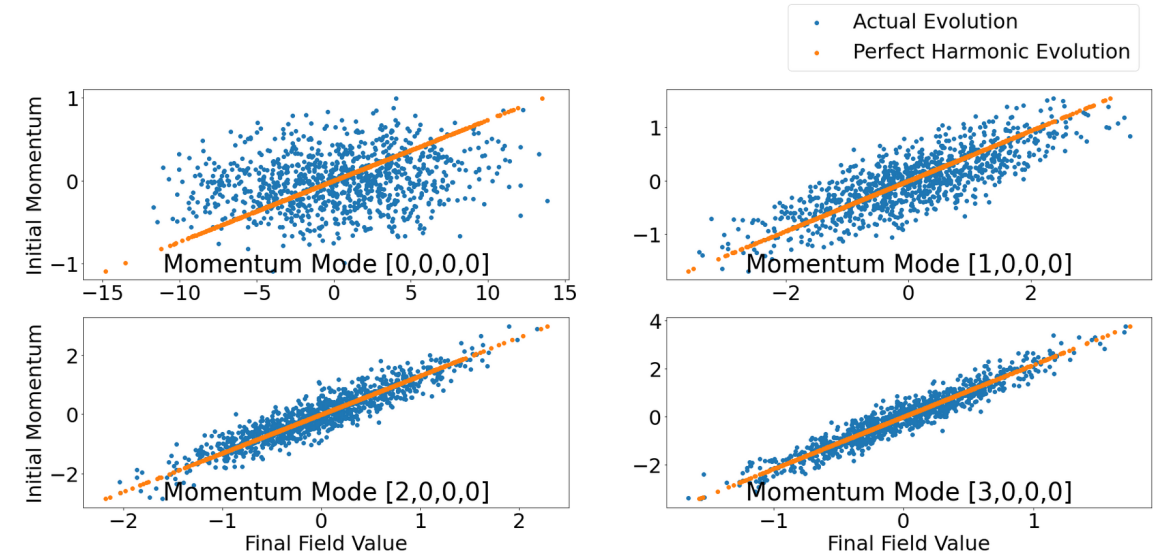
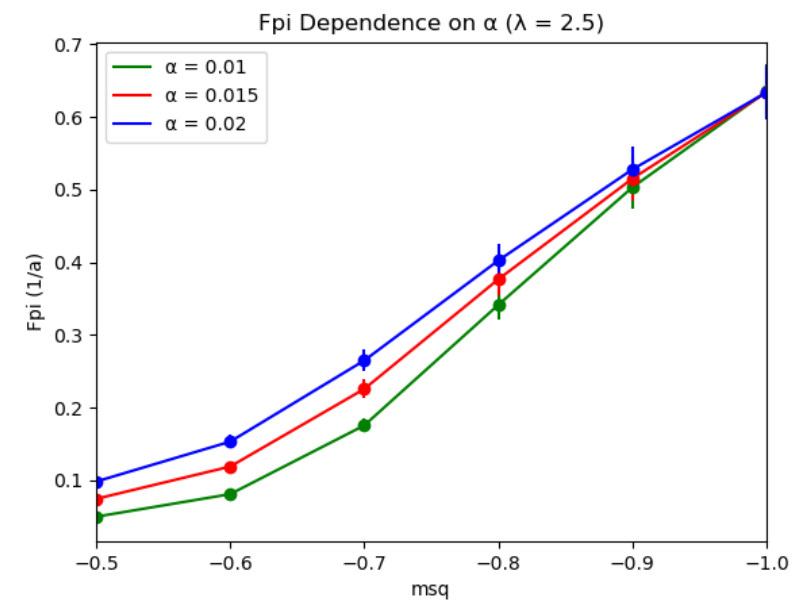
Abstract: The linear sigma model is a low energy effective model of Quantum Chromodynamics. This model mimics the breaking of chiral symmetry both spontaneously and explicitly through the quark condensate and pion mass matrix respectively. Fourier acceleration is a method that can be implemented in the Hybrid Monte-Carlo algorithm which decreases autocorrelations due to critical slowing down through tuning the mass parameters in the HMC algorithm. Fourier acceleration is applied to the linear sigma model with a novel mass estimation procedure, by assuming the modes behave approximately like simple harmonic oscillators. The masses are chosen by sampling the expectation values of <Pi> and < phi_i(p) – nu*delta_{i,0}*delta_{p,0}> (auxiliary momentum, and vacuum expectation of the fields) generated by the HMC algorithm. Additional findings in the linear sigma model during exploration of the symmetry breaking point are also discussed.
Preprints
Abstract: The security of two-way entanglement purification protocols has been closely studied, the security of one-way entanglement purification has comparably received less attention. Therefore, in this paper we propose a one way entanglement purification protocol and prove its security using the properties of error correcting codes, as one way entanglement purification protocols are equivalent to error correcting codes. We use the paradigm of quantum sampling introduced by Bouman and Fehr to estimate the classical Hamming distance error of the qubits which passed through the channel. We can use this estimated Hamming distance δ to determine the amount of interference that Eve has subjected to the quantum channel. Using quantum sampling, we can prove that if Eve’s attacks are restricted to Pauli gates, we can disentangle Eve from the message through an error corrected code of size (d−1)/2 = 2δ with probability 1 − ϵ. We also expand this to include measurements and qubit resets or interceptions by Eve as well. We hope that this approach may be expanded to arbitrary single and multi-qubit gates to obtain more general security guarantees for similar one-way entanglement purification protocols.
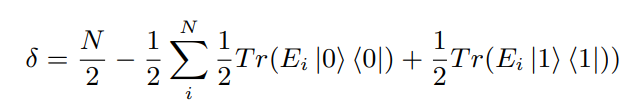
Abstract: The quantum-Extended Church-Turing thesis has been explored in many physical theories including general relativity but lacks exploration in quantum field theories such as quantum electrodynamics. Through construction of a computational model whose gate set mimics the interactions of QED, we demonstrate that one of the defining features of quantum field theory, particle creation and annihilation, is not likely to violate the quantum-Extended Church-Turing thesis. Through this computational model, it is shown that particle creation is likely only another form of quantum parallelism. However, whether or not the quantum-Extended Church-Turing thesis will hold for all computational devices in quantum field theories is still not known. For example, we briefly examine certain interactions in quantum electrodynamics which may create multi-qubit gates. These gates may have exponential complexity at the cost of being exponentially weak. This may in turn allow for computational advantage over traditional gate sets such as Clifford+T.
Other Projects
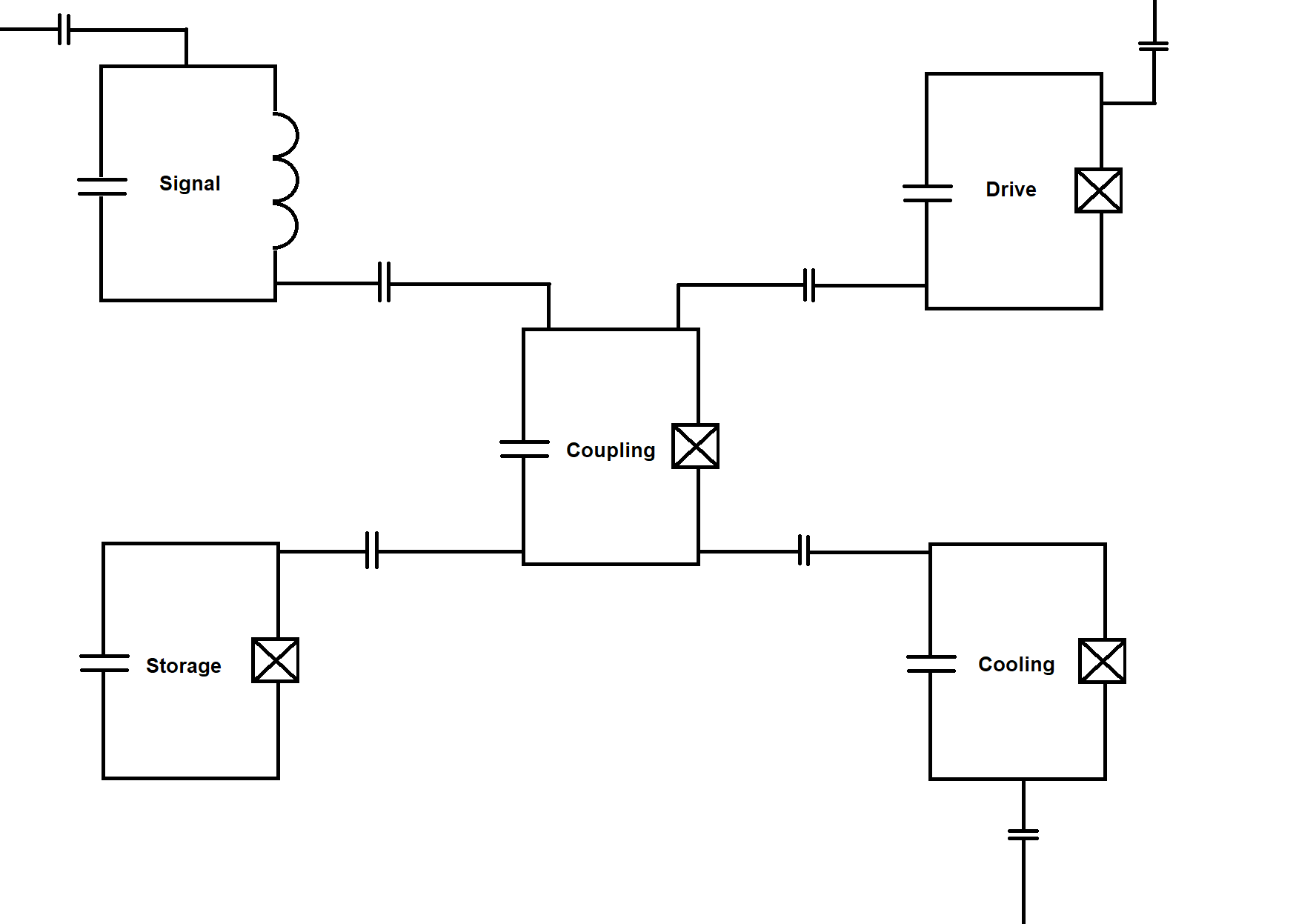
Abstract: Quantum Amplifiers are an important part of superconducting quantum devices. In this paper we design a novel superconducting amplification circuit. This circuit is designed using only qubits and resonators and can therefore be intuitively understood through tracking excitations through these circuit elements. We simulate the designed circuit using QuTiP and show that the first round of amplification is 80% efficient. However, multiple rounds of amplification do not increase the expected number of photons in the signal resonator as the likelihood of relaxation surpasses amplification. This relaxation is due to the cooling qubit, which allows for excitations to leak from the storage, signal, and drive qubits. Increasing the efficiency of amplification from 80% will allow for a greater number of maximum photons in the amplification resonator before relaxation dominates behavior of the circuit.