Does Quantum Field Theory have more computational power than Quantum Mechanics?
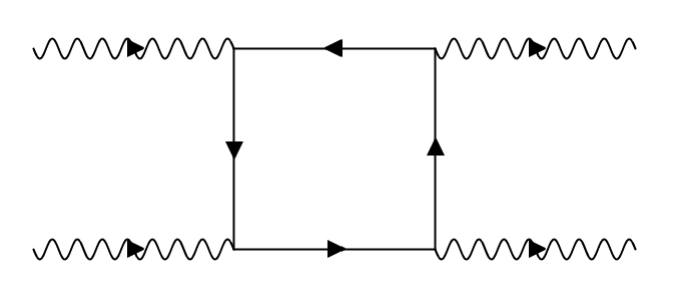
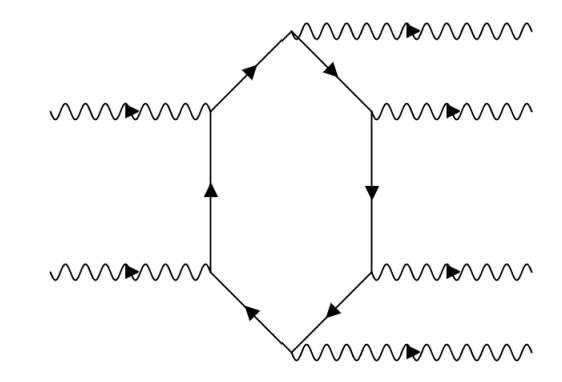
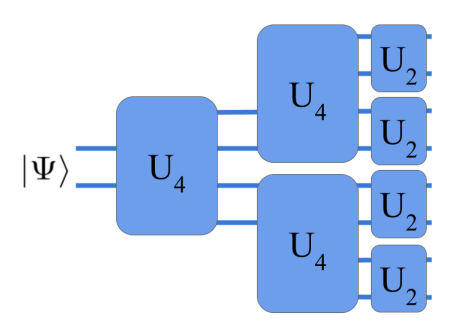
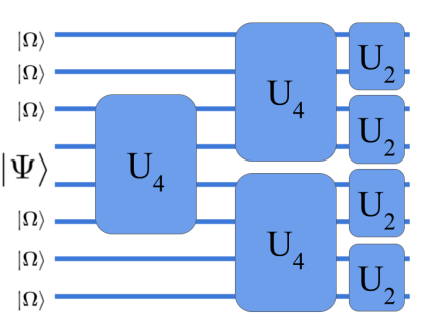
In this paper I begin to address this question through the construction of a gate-based computational model whose gates mimic the interactions of Quantum Electrodynamics. More specifically, I use fourth and sixth order Feynman diagrams to motivate the inclusion of two-qubit and two-to-four qubit gates in this computational model, the latter of which allows for the model to realize particle creation.
I then demonstrate that the computational model created can be simulated by a qutrit quantum computer with access to exponentially many ancilla qutrits. This finding implies that the two-to-four qubit particle creation gate does not allow for the computational model constructed to gain an advantage over traditional quantum computers. This finding is interesting since it suggests that particle creation in Quantum Field Theory may not provide any significant computational advantages.
However, particle creation is not the only feature of Quantum Field Theory not shared by Quantum Mechanics. Through further examination of the constructed computational model, we can see that the model can be efficiently simulated by a quantum computer since its gates have fixed size. However, Quantum Field Theories such as QED allow for interactions which scale with the system size, at the cost of being exponentially suppressed by the coupling constant. This motivates investigation into a class of exponentially suppressed mutli-qubit gates. This class of gates put forth are at least restricted by the coupling constant by the equation Tr(I-U) < O(e^N). However, these gates may be further restricted by other structures or theorems in Quantum Field Theory as well.
Examining the successes of quantum computing demonstrates that this class of gates may provide computational advantage. The Gottesman-Knill Theorem shows that it is not solely superposition and entanglement which gives quantum computers their computational power. Instead, Shor’s algorithm demonstrates that exponentially small finely-tuned gates give computational advantage to quantum computers. This suggests that it may be possible to find computational advantage with these exponentially suppressed multi-qubit gates.
However, it is necessary to warn that this class of gates may not be fully realizable in Quantum Field Theory. Many theorems restrict the allowed interaction in Quantum Field Theory and therefore if computational advantage is identified, the necessary gates must then be constructed in a Quantum Field Theory. This work has been submitted to ArXiv, click the button below to read the paper.